
Sample Maths SATs Questions and Answers: Arithmetic
Bookmark this page? Pop your email into the box below to receive a link to this article so you can easily refer back to it later.
Table of Contents
Introduction
The maths SATs papers cover the entire breadth of the subject across both Key Stages. Children taking the paper can expect to come up against a wide variety of question types, ranging from straightforward arithmetic to more complex, multi-step problems.
The following examples have been chosen to give you a good understanding of the types of questions that your child may face on the day of the test. We’ve also included some hints and tips for maximising the potential of scoring full marks on each one. All questions are taken from the most recent tests, which were administered this year.
Maths SATs Sample Question 1
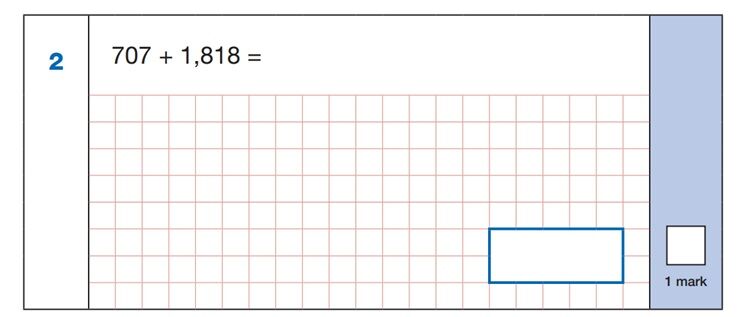
Initially, this might seem like a straightforward addition question. However, bearing in mind that there are 36 questions in the arithmetic paper and that children only have 30 minutes to answer them all, the question actually requires swift working.
In the given example, children may default to writing out the calculation using a formal written method (column addition). However, this can take precious seconds to do. A more effective alternative would be to answer the question using mental calculation/jottings. For example, if the child can count in hundreds, they could start at 1,800 and count on seven hundreds: 1,900, 2,000 (at this point they may even be able to add the remaining five hundreds) 2,500. 18 + 7 = 25, and adding this to the previous total would give 2,525.
This kind of mental agility is extremely beneficial when faced with apparently ‘simpler’ question types and may save valuable time that can be used later, on much harder questions.
Maths SATs Sample Question 2
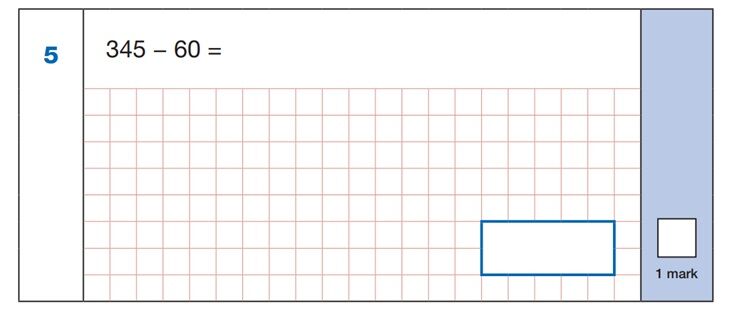
Again, here is an opportunity to save valuable time. Setting this calculation out in a formal way would take quite a lot of effort, as well as increasing the risk of making a mistake (either in the setting out or in using the decomposition method).
If a child recognises that 60 is the same as 45 + 15, they can complete the subtraction in two stages: 345 – 45 = 300. 300 – 15 = 285.
When checking the calculation, children should aim to use the inverse, or opposite operation, i.e. 285 + 60 = 345.
Maths SATs Sample Question 3
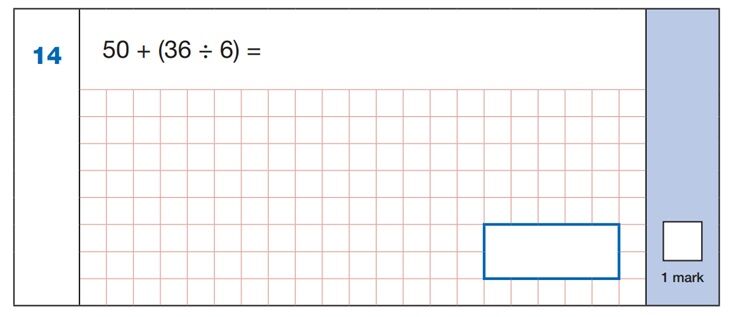
This question relies on a secure understanding of the BIDMAS rule for operations, whereby the order of a calculation should be Brackets, Indices, Division, Multiplication, Addition and finally, Subtraction. For the calculation shown, everything within the brackets should be calculated first, so 36 ÷ 6 = 6, and then the addition, 50 + 6.
Maths SATs Sample Question 4
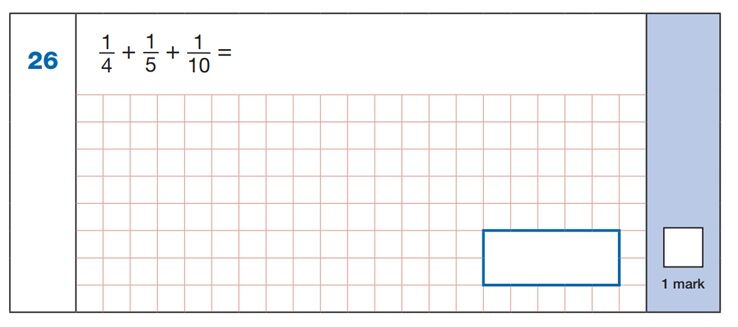
Solving this calculation relies on an understanding of the rules of fractions. In this particular case, we cannot add the fractions together as they have different denominators. To find a common denominator, the child should find the lowest common multiple of all three denominators (in this case 20).
They should then adjust each numerator by recognising what happened to the denominator to turn it into 20. For example, to turn 4 into 20, it must be multiplied by 5.
The same operation should be carried out on the numerator, meaning the 1 should be multiplied by 5 also, resulting in a fraction of 5|20. This rule is applied to all three fractions, resulting in three which have a common denominator of 20.
The fractions can then be added together and the resulting answer of 11|20 is in its lowest form, requiring no further adjustment.
Maths SATs Sample Question 5
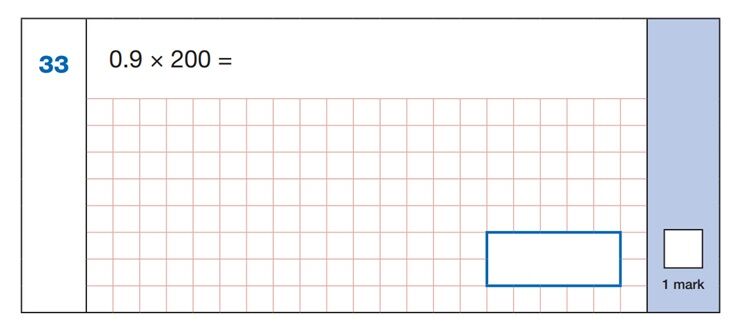
There are two main ways to solve this calculation, and both require a secure understanding of place value. The first method could be to recognise that 0.9 x 2 = 1.8 and then, as the 2 is actually 100 times larger, the answer would be 180.
The second way of solving the question could be to calculate 0.9 x 100 and then to double the answer. Again, children who may be tempted to write out the calculation in a more formal way should consider the time this may take and try a mental approach if possible.
Maths SATs Sample Question 6
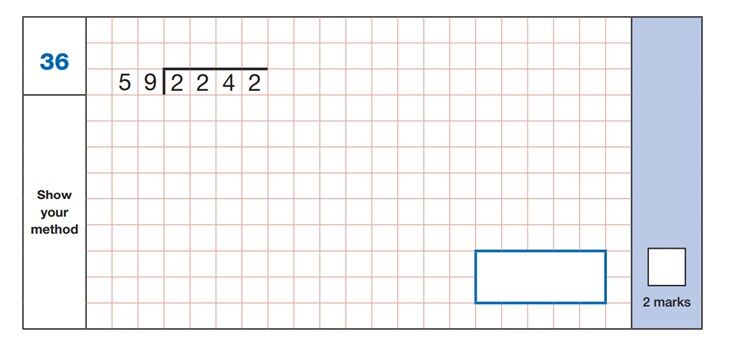
This question is worth two marks – two marks would be awarded for an entirely correct answer (even without any working out shown!) or, in the event of an incorrect answer, one mark may be awarded for a correct method applied to the working out.
The most likely method here would be to use ‘chunking’, or repeated subtraction of groups of 59 until there is a result of either zero or a remainder. Children should try to use easier groupings of the number and recognise that if they know 10 x 59 = 590, then 5 x 59 would be 295 and 20 x 59 would be 1080.
The fastest and most straightforward method for most children might be 20 x 59, 10 x 59, 5 x 59, 3 x 59 (or possibly 1 x 59 three times) to achieve an answer of 38.
Hopefully, the explanations of these arithmetic SATs questions have provided you with some insight into the level your child will be expected to achieve in their exam. As time is of the essence, it’s important that students identify time-saving methods to answer questions.
Our SATs Resources
In order to give your child the best chance of performing well in their SATs, you should consider giving them extra practice with SATs practice exam papers. At Exam Papers Plus, we have a range of SATs papers that cover the entire SATs curriculum, including the Maths elements.
Not only are our practice papers up-to-date, but the contain detailed marking schemes, so you can chart your child’s progress throughout their studying. To help your child prepare for the Maths SATs exams, we’d recommend the following resources:
Key Stage 1: SATs Practice Test 1
Key Stage 1: SATs Practice Test 2
Key Stage 2: SATs Practice Test 1
Key Stage 2: SATs Practice Test 2
Related posts:
How to Score Highly in the SATs Tests
Bookmark this page? Pop your email into the box below to receive a link to this article so you can easily refer back to it later.
















